T-Test (one sample)

The t-test shows if your expected mean assumption is reasonable or not. With a t-test you try to answer the following question: How likely is your mean estimate (eg. 1,36%), if the mean of the total population would be..% (eg.1,5%) -> in other words is your sample mean close enough to the total popultion mean that you can assume for all of your population the total population mean is right?

So you ask yourself: Is my expected mean correct (on average)? -> Therfore you would use that as your null hypothesis. 

Example:
EM funds proivde on average a montly retrun of 1,5% in 2019 -> This is my null hypothesis

As you can asume, there are a lot of EM funds. Therefore we just draw a sample of 5 funds with the returns:
1%; 1,3%; 3,2%; 0,1%; 1,2%
1) Now lets calculate the mean:
6,8%/5=1,36%
2) Now lets calucultate the variance:
The variance is ((x-xI)/n-1)^2 
((1-1,36)+(1,3-1,36)+(3,2-1,36)+(0,1-1,36)+(1,2-1,36)/(5-1))^2 = The variance is 0,0144
1,36% close enough to 1,5% that one can keep that value for the total population ? Cause as you can imagine if we take a sample of 5 other funds we most likely get a different mean.

Therefore your sample shoud have a big enough size.  

Formula:

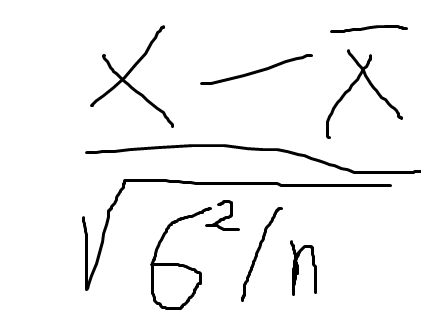
Formula: (Mean (sample population) – Mean (total poulation)) / (sample variance/size sample)^(1/2)

Step 1: Enter values in formula

((1,36-1,5)/(0,0144/5)^(1/2)) = -2,61 ->t value

Now compare that t value with the critical value (use respective confidence level e.g. 90%)

Critical value (alpha half=5%) -> -1,645

Therefore our t value is bigger than the critical value- > We reject the null hypothesis. Our alternative hypothesis is: The return of EM funds does differentiate from the mean of 1,5%