Standard normal distribution

As one would probably expect, the standard normal distribution is standardized.

When working with distributions, one usually looks for intervals within which a value lies. E.g., One is asking: With which probability a value y lies between y1 <y < y2 ?

Standard normal distribution is the best way to calculate such a probability.

First, you standardize your y values to z values.

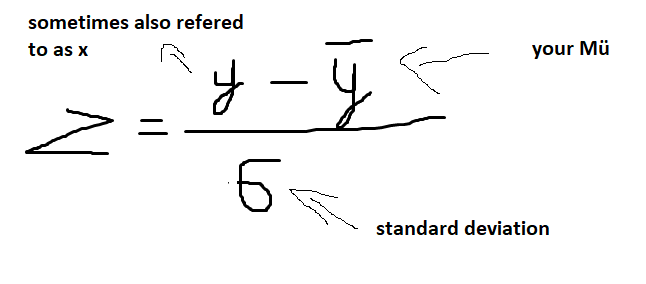
If you found the z value look for the Phi value in the z table (which you can find on the internet). The Phi value tells you the probability from -infinite till this z value.

Example 1

Which value of the variable y has fallen bellow with a probability of 10%?

Given probability 10%
Standard deviation 6,00
Mean (Mü) 0,5
Now you have your formula: z = (y-yI)/stand. 
As outlined above, by looking at your z value, you can find the respective Phi value. So, of course, you can find the respective z value with a Phi value.
 
Formula: 10% -> z= -1,2582
-1,2582 = (y-0,5)/6
-1,2582*6+0,5= y
y = -7,05
A y value of -7,05 will be fallen bellow with a probability of 10%. 

EXAMPLE 2
Which value of the variable y has excceded with a given probability of 10%?

Given probability 10%
Standard deviation 6,00
Mean (Mü) 0,5
Formula: z = (y-yI)/stand 
phi*stand+yI = y 

The Phi value tells you the probability from minus -1 till this z value. You look for an excceding value, so you must find the phi value (probability) that a variable y would fall bellow with a given probability of 90% (100%-10%).
90% has a z value of 1,282.
1,282*6+0,5 = 8,192

Therefore, the value of the variable y that is excceded with a given probability of 10% is 8,192.

Example 3
In which range (interval) is a given proportion ( 90%) of the data?
Given probability: 5% on the left side and 5% on the right side. 

Standard deviation 6,00
Mean (Mü) 0,5
You do this for both z values. z1 and z 2

First, let's calculate the 5% area on the left. As you know, Phi always shows you the probability from -infinite till the z value. The z value for 5% is -1,645.
Now we calculate the z value on the right. 100%-5% = 95%. The z value for 95% is 1,654

Formula= Z*stand+yI. = y

y= 1,645*6+0,5= 10,37. That means 95% of the values excede 10,37

Formula= z*stand+yI=y -> y= -1,645*6+0.5 = – 9,37. That means 5% of the values are bellow -9,37.

Therefore 90% of the values are between -9,37 and 10,37!