Confidence intervals
The confidence interval shows you an interval within which the actual (presumed but unknown) mean of a population lies within a specified probability of 1-Alpha. (Alpha is the risk of making a wrong decision eg. 1% in case of a 99% confidence interval)
You can define different confidence intervals ( eg. a confidence interval of 90% or 99%)
If we find out that in respectively at least 90% or 99% of cases our assumption is right then we keep our null hypothesis.
If you want to calculate a confidence interval you need to follow these steps:
First, define the mean.
Second, define the borders (z values) of the interval.
Third, calculate the variance Formula: ((y-yI)^2/(n-1)). After that, calculate the standard deviation Formula: (variance)^(1/2)
Fourth, enter these values in the formula for the confidence interval:
Formula Convidence Interval:
x1 = (mean – z (lower border) * (standard dev./(n^(1/2)))
x2 = (mean + z (upper border) * (standard dev./(n^(1/2)))
z = alpha half quantil cause we do a 2 sided test
Example:
Mean (sample): 10%, n=123, Variance: 0.2
We want to analyze a null hypothesis that states that the mean of the (total) population is 13%. We use a confidence interval of 90%.
So first we make an assumption we want to test if based on our sample the average size of the total population mean can be 13%.
So we analyze the sample and if we find out that in at least 90% of cases our assumption is right then we keep our null hypothesis (assumption)
Formula: Mean+z*(stand/n^(1/2))
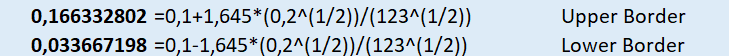
As you can see the total population mean of 13% (=0.13) is within the 90 % confidence interval. We can’t falsify our null hypothesis, therefore we keep our null hypothesis (assumption).
Example 2
Now we use a confindence interval of 99%
0,1+2,576*(0,2^(1/2))/(123^(1/2)) -> Upper border of 99% quantile is:
| 0,20387435 |
0,1-2,576*(0,2^(1/2))/(123^(1/2)) -> Lower border of 99% quantile is:
| -0,003874346 |
As you can see the 99% confidence interval is bigger than the 90% confidence interval. Why ?
This is because the confidence interval of 99% has to include the mean of the population with a probability of 99% the confidence interval of 90% has to include the mean of the population only with a probabilty of 90%.
Simply said one can be wrong 10% with a 90% confidence interval and just 1% with a 99% confidence interval. So we need a bigger interval that it’s more likely that we are wrong just 1%.
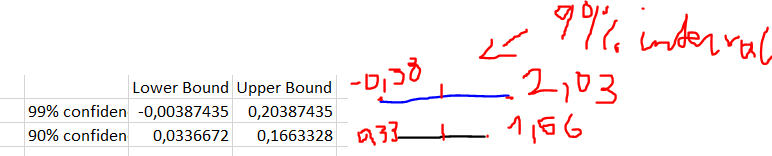
The confidence interval has the same size on both sides of the sample mean.