The value of money at different times

IIf you buy a bond, you become a lender to the bond issuer. In return for lending money, you, in many cases, receive interest payments. Against this background, one should remember that the interest payments one gets closer to today are more valuable than those one receives in the distant future. E.g., if you get one euro tomorrow, it is better than if you get one euro in one year.

Therefore, it is essential to discount or compound interest payments adequately – depending on whether one wants to calculate an investment’s present or future value.

Let’s start with the future value: To calculate the future value, we need to compound interest payments.

Future value at time n (Etn) = Present value(Pt) * (1+r)^ⁿ

Example: Imagine you have 200 Euro today. You decide to buy an EM bond which pays you a coupon of 15% each year for 5 years.

Preset Value (Pt0): 200 Euro
Future value (Ft5): ?
Interest p.a. (r): 15%

Insert the numbers in the formula for the future value: Ft5= 200 *(1+0,15)^⁵ = 402,27 Euro.

That means the future value (= the value of your investment in 5 years) is 402,27 Euro.

If you have the future value and you want to know the present value you have to discount the interest payments.

Formula prestent value:

Future value / (1+r)^ⁿ = Present value –> you can also write this as ->

Future value * (1+r)^^-n = Present value

Example: You know the future value (end value) of a bond and you want to calculate the present value.

Present Value (Pt0): ?
Future value (Ft5): 400 Euro
Interest (r): 15%

Insert the numbers in the formula for the present value:

=400*(1,15^(-5)) = 198,87

That means the present value (= the value of your investment in at the start) is 198,87 Euro.

By now, it is clear that (1+r) is your capital’s (annual) growth rate. Therefore, we can transform the formula for the future value and use the same numbers:

(Future value / Present value)^(1/n) -1 = r

(400/ 198,87)^(1/5) -1 = 0,07 (7%) = r

Our investment grew by 7% a year.

Fixed-rate bonds are the most common bond type. Their primary characteristic is that the bond holder receives interest payments (coupons) at specified times. (Which are mostly yearly in Europe)

Discount factor

If you have a row of equally sized future payments (which you get at the end of each period) and want to know what all these are worth today, then you need to discount these future payments.

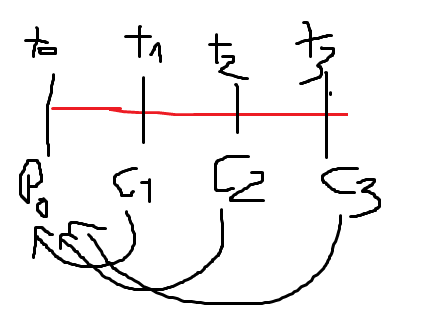
Present value (P0)= payment (c) * discount factor

Discount factor = ((1-(1+r)^(-t_n)/i))

Example:

You have three payments (c) at three future dates (t)
t1 = 10, t2 = 10, t3 = 10
and an interest rate (i) of 15%

Enter these values in the present value formula

10 * (1-(1+0,15)^(-3))/0,15 = 22,83

Today the 3 payments are worth 22,83 Euro