Arithmetic mean vs geometric mean
Mostly when you talk about the average you actually talk about the arithmetic mean. The arithmetic mean is useful if one wants to look at independent variables. Eg. for the average income of 2 different lawyers.
2000 Euro + 4000 Euro / 2 Lawyers = Lawyers average =3000 Euro
The geometric mean ensures that the ratio of each number towards the geometric mean number is the same.
Formula geometric mean: (1+r1*1+r2*1+rn)^(1/n)
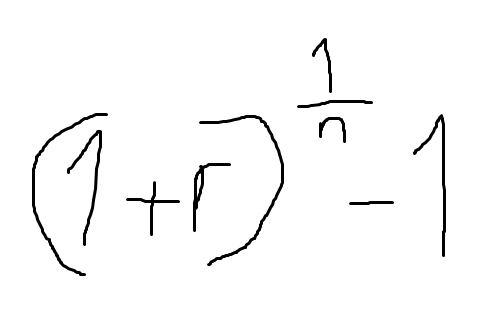
Example we have 2 numbers. 2 + 8
(2 x 8)^(1/2)= 4
Let’s check the ratio. First we look at the ratio of the smaller number and the geometric mean -> 2:4= 1/2 (ratio)
And then we look at the ratio of the geometric mean to the bigger number 4/8 = 1/2 (ratio)
As you can see they are both ratios 1/2.
The geometric mean is usually used when we want to take into account the compound rates in the past.
Eg we have 2 different interest rates:
1 year 2%
2nd year 3%
We take the formula (we need to use gross returns).
((1+0,02) * (1+0,03) =1,025
Our geometrical mean is 2,5%
Example we have an Emeriging Markets Index with the following prices
| Price Index | Discrete return |
| Day1: 1 | Formula: ((price today) – (price day before))/(price day befoe) *100 |
| Day2: 2 | (2-1)/1*100 = 100%. As you can see the Price of the index rose from day 1 from 1 to 2 on day 2. So the return is 100% |
| Day3: 3 | 51,00 % |
| Day4: 4 | 34,33 % |
| Day5: 5 | 26,00 % |
| Day6: 6 | 21,00 % |
| Day7: 5 | -15,67 % |
| Day8: 7 | 41,00 % |
| Day9 :6 | -13,29 % |
| Day10: 7 | 17,67 % |
| Day11: 8 | 15,29 % |
| Day12: 9 | 13,50 % |
| Day13: 10 | 12,11% |
Now we write the the returns in decimal format and add +1 to get the gross return
| 1,00 +1 |
| 0,50 +1 |
| 0,33 +1 |
| 0,25 +1 |
| 0,20 +1 |
| -0,17 +1 |
| 0,40 +1 |
| -0,14 +1 |
| 0,17 +1 |
| 0,14 +1 |
| 0,13 +1 |
| 0,11 +1 |
2) Now you multiply these 12 returns with each other.
2*1,5*1,33*1,25*1,20*0,83*1,40*0,86*1,17*1,14*1,13*1,11 = ~ 10
3) Lets insert our result in the formula for the gemoetric mean
Formula (1+r)^(1/n)
Therefore 10^(1/12) = 1,21..
Now you have to subtract -1 and multiply the result with 100 to get the net return in % -> 21,..% is the geometrical mean return of our EM index.